1. Home
  2. Blog
  3. The CARLA Coordinate System

The CARLA Coordinate System

Nov 19, 2023 By Han Wu

A summary of CARLA Coordinate System (Global, Camera, Image).

Introduction

To project the location of a 3D vehicle $O_{world}=(x, y, z, 1)$ onto the 2D camera image $O_{image}=(u, v, w)$, we need to be familiar with the CARLA coordinate system.

$$O_{image} = K[R|t] O_{world}$$

  • Global Coordinates: $O_{world}$ is available using the API vehicle.get_location();
  • Extrinsic Matrix: $[R|t]$ is provided by the API camera.get_transform().get_inverse_matrix();
  • Intrinsic Matrix: $K$ can be constructed from camera properties (w, h, fov).

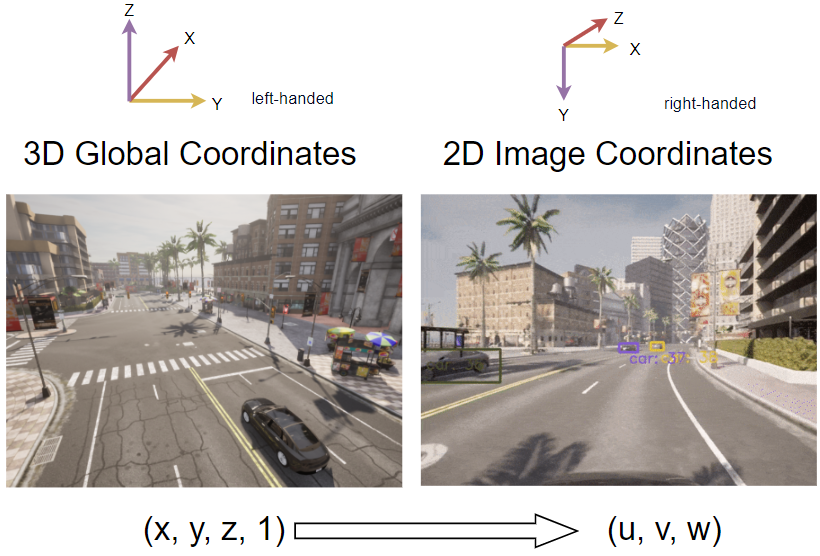
Global Coordinate

CARLA is developed using the Unreal Engine, which uses a coordinate system of x-front , y-right , z-up (left-handed).

We can get the world location (x, y, z, 1) of a vehicle using the API vehicle.get_location().

1>> vehicle.get_location()
2<carla.libcarla.Location object at 0x0000020E1CF58A50>
3x: -110.14263153076172
4y: -7.242839813232422
5z: -0.005238113459199667

Extrinsinc Matrix

The extrinsic matrix calculates the position of a vehicle relative to the camera.

$$O_{camera} = [R|t] O_{world}$$

1# Get the extrinsic matrix 
2world_2_camera = np.array(camera.get_transform().get_inverse_matrix())

Intrinsic Matrix

We also need the intrinsic matrix K to project the relative position $O_{camera}$ to image coordinates $O_{camera} = (u, v, w)$.

$$O_{image} = K O_{camera}$$

Intrinsic Matrix:

$$ K = \begin{bmatrix} f & 0 & \frac{w}{2} \\ 0 & f & \frac{h}{2} \\ 0 & 0 & 1 \end{bmatrix} $$

 1def build_projection_matrix(w, h, fov, is_behind_camera=False):
 2    focal = w / (2.0 * np.tan(fov * np.pi / 360.0))
 3    K = np.identity(3)
 4
 5    if is_behind_camera:
 6        K[0, 0] = K[1, 1] = -focal
 7    else:
 8        K[0, 0] = K[1, 1] = focal
 9
10    K[0, 2] = w / 2.0
11    K[1, 2] = h / 2.0
12    return K

Full Example:

Example 07: https://github.com/wuhanstudio/carla-tutorial

 1def get_image_point(loc, K, w2c):
 2    # Calculate 2D projection of 3D coordinate
 3
 4    # Format the input coordinate (loc is a carla.Position object)
 5    point = np.array([loc.x, loc.y, loc.z, 1])
 6    # transform to camera coordinates
 7    point_camera = np.dot(w2c, point)
 8
 9    # New we must change from UE4's coordinate system to an "standard"
10    # (x, y ,z) -> (y, -z, x)
11    # and we remove the fourth componebonent also
12    point_camera = np.array(
13        [point_camera[1], -point_camera[2], point_camera[0]]).T
14
15    # now project 3D->2D using the camera matrix
16    point_img = np.dot(K, point_camera)
17
18    # normalize
19    point_img[0] /= point_img[2]
20    point_img[1] /= point_img[2]
21
22    return point_img
CARLA